E.Str.A.D.A. - Studenti
UNITA' 3: AZIONI INTERNE E DIAGRAMMI
Ing. Paolo Rugarli
Abbiamo visto come si possa sempre ricondurre una struttura isostatica alla situazione che vede un certo numero di azioni e reazioni applicate in vari punti della struttura, facendo sì che tutte le equazioni di equilibrio vengano rispettate.
Ci si pone ora di fronte un nuovo problema: che genere di prova rappresentano le azioni applicate per la struttura? Sarà essa in grado di sostenere queste azioni oppure no?
Per poter rispondere a queste domande è necessario conoscere, in ogni punto della struttura, il valore degli sforzi normale e tangenziale.
Nella prima parte del corso si è visto in che modo, partendo dalle azioni interne si possano calcolare questi sforzi normale e tangenziale, e si è anche visto come si possa decidere se gli sforzi calcolati siano o meno sopportabili. Si tratta dunque si capire come si possano calcolare le azioni interne, azione assiale N, taglio T, momento flettente, M, a partire dalle forze attive e reattive applicate.
Consideriamo a titolo di esempio la struttura seguente già vista nella precedente lezione.
Abbiamo detto che l’azione del vincolo a terra può essere assimilata alla applicazione delle reazioni vincolari nel punto ove il vincolo agisce.
E’ intuitivo che la struttura faccia in qualche modo da tramite tra il carico applicato ed il vincolo, cosicchè anche essa si venga a trovare coinvolta nel compito di “portare” il carico applicato. Per capire come, osserviamo che considerato un generico punto distante “x” dall’estremo caricato, in quel punto si può immaginare siano saldati due pezzi dell’asta in oggetto: quello cha va dal carico al punto e quello che va dal punto al vincolo.
Due pezzi saldati equivalgono a due pezzi incastrati tra loro. Abbiamo già imparato che ai vincoli si possono sostituire le loro reazioni, pur di calcolare queste ultime in modo da rispettare l’equilibrio. Non dobbiamo fare altro che ricordare il principio di azione e reazione, che sancisce che quando un corpo esercita su un altro una certa azione, quest’altro esercita sul primo una reazione eguale in modulo e contraria in verso. Possiamo dunque tagliare l’asta nel punto che dista x (un punto assolutamente generico) dall’estremo libro pur di:
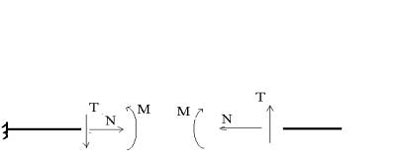
1) Evidenziare le azioni interne (tre perché abbiamo soppresso un incastro) N, M, T sul lato ad esempio destro, e –N, -M, -T sul lato sinistro, e si noti che benchè di segno opposto sui due monconi, le reazioni evidenziate provocano su ciascun moncone sempre lo stesso effetto fisico. Se le mettiamo, per esempio, con le ordinarie convenzioni di segno, N provoca una trazione, T uno scorrimento orario, M la trazione delle fibre inferiori;
2) Imporre che il pezzo di destra (o in alternativa quello di sinistra) siano in equilibrio sotto le forze note e le nuove reazioni N, T, M, incognite.
Le azioni scambiate dalle due parti nel punto interno si chiamano dunque azioni interne: esse variano da punto a punto ed è grazie al loro insorgere che la struttura può sopportare i carichi applicati. Si pensi: in loro assenza nessuno dei due pezzi potrebbe rimanere in equilibrio sotto le azioni applicate, e l’asta perderebbe la sua integrità.
Ecco dunque in che modo potremo, in generale, conoscere le azioni interne N, M, T, in un generico punto, di una generica asta, di una generica struttura sottoposta ad un generico insieme di azioni applicate:
1) Ridurremo la struttura ad albero in modo da escludere la presenza di cicli chiusi;
2) Tagliaremo l’albero in due part mediante sezione proprio nel punto ove siamo interessati a conoscere le azioni interne;
3) Evidenzieremo le azioni interne incognite su ambo le parti risultanti, con i versi opposti;
4) Scriveremo tante equazioni di equilibrio indipendenti per le parti ottenute col taglio quante sono le azioni interne incognite
5) Risolveremo il sistema corrispondente.
Se applichiamo queste regole all’esempio precedente, otteniamo i seguenti passaggi:
1) La struttura è già ridotta ad albero, le reazioni, inoltre sono già state calcolate.
2) Tagliamo l’asta in un generico punto distante “x” dall’estremo libero (il fatto che la distanza sia genericamente x, e non un numero preciso sta proprio a significare che si tratta di un punto generico).
3) Evidenziamo le azioni interne, N, M, T, seguendo le consuete convenzioni: l’azione assiale positiva se tira i due monconi; il taglio positivo se provoca una distorsione oraria; il momento flettente positivo se provoca una concavità verso l’alto (“tende le fibre di sotto”).
4) Scriviamo l’equilibrio per esempio del moncone di destra:
Se risolviamo questo semplice sistemino troviamo:
Poiché abbiamo usato un punto generico, e poiché avremmo scritto lo stesso sistema di equazioni in qualunque altro punto sull’asta (non intervenendo altri carichi applicati), le espressioni trovate rappresentano le azioni interne in tutti i punti dell’asta.
Se rappresentiamo ciascuna di esse in un diagramma riportato sullo stesso asse dell’asta, dove in ascissa ci sono i vari punti dell’asta ed in ordinata il valore della azione interna, otteniamo i diagrammi seguenti (il diagramma di momento è sempre riportato, per convenzione, dalla parte delle fibre tese ad opera del momento stesso, in pratica dalla parte dove il momento genera una convessità):
I diagrammi sono molto utili ed amplissimamente usati nella pratica, poiché ci dicono come variano le azioni interne lungo l’asta, facendo vedere le sezioni dell’asta più sollecitate. In questo esempio è chiaro che la sezione più sollecitata è proprio quella dell’incastro, poiché il taglio e ovunque eguale, mentre il momento flettente cresce linearmente all’avvicinarsi all’incastro (M=pLx).
Vediamo un secondo esempio.
In pratica è l’esempio precedente con l’aggiunta di una forza distante L/3 dall’incastro. La soluzione porta alle seguenti reazioni ed ai seguenti diagrammi:
Il calcolo delle reazioni vincolari lo lasciamo come esercizio. Chiamiamo V la reazione verticale, R la coppia antioraria.
Rompiamo l’asta in un punto generico e scriviamo le equazioni di equilibrio (sempre alla traslazione orizzontale, a quella verticale, ed alla rotazione intorno all’asse passante per il punto di rottura). Osserviamo che le equazioni di equilibrio cambiano a seconda che ci si trovi tra l’incastro e la prima forza o tra la prima forza e l’estremo. Nel primo caso, con le solite convenzioni, scriviamo (x parte ora da sinistra)
Se 0<= x <= L/3
N=0
T – V = 0
R-Vx+M=0
E poiché V=pL ed R=1.3333 pL2,
T = 2pL
M = 2pLx – 1.3333pL2
Nel secondo caso scriviamo
Se L/3<= x <= L
N=0
T = V-pL= 2pL-pL=pL
M = Vx – R – pL (x-L/3) = 2pLx – 1.3333pL2 – pL(x-L/3)
La rappresentazione grafica delle curve N(x), T(x), M(x) altro non è che il diagramma della corrispondente componente di azione interna.
L’applicazione di una nuova forza ha modificato le reazioni vincolari ed i diagrammi.
In generale, percorrendo l’asse di un’asta, tutte le volte che si incontra una nuova forza o una nuova coppia, i diagrammi subiscono dei cambiamenti di forma. Precisamente si può dire che:
1) Quando si incontra una forza diretta come l’asse dell’asta l’azione assiale ha un salto brusco pari al valore della forza applicata;
2) Quando si incontra una forza diretta perpendicolarmente all’asse dell’asta il taglio ha un salto brusco (discontinuità di prima specie in termini rigorosi) ed il diagramma di momento una cuspide (discontinuità di seconda specie, o punto angoloso);
3) Quando si incontra una coppia concentrata il diagramma di momento ha un brusco salto di valore pari al modulo della coppia incontrata;
4) Nei tratti di asta sui quali non è applicato un carico uniformemente distribuito il taglio e l’azione assiale hanno andamenti costanti, il momento flettente varia linearmente;
5) Nei tratti d’asta sui quali è applicato un carico uniformemente distribuito perpendicolare all’asse dell’asta l’azione assiale è costante, il taglio ha andamento lineare ed il momento andamento parabolico, con concavità opposta al verso del carico distribuito applicato (vedremo in seguito un esempio).
Tutti questi risultati si possono facilmente dimostrare. Inoltre si può dimostrare che la derivata del momento flettente coincide con il taglio, la derivata del taglio coincide con il carico distribuito applicato, in ogni punto di ascissa “x” sull’asse di una trave che sia rettilinea. In formula:
T(x)= M’(x) = dM/dx (1)
p(x) = -T’(x) = -dT/dx (2)
e quindi
p(x) = -M’’(x) = -d2M/dx2 (3)
Ecco dunque, ad esempio, perché ad una cuspide nel diagramma di momento corrisponde (basta vedere i diagrammi dell’ultimo esercizio) un salto nel diagramma del taglio: la derivata del momento, la sua pendenza, cambia in una cuspide. Bene, poiché tale derivata è eguale al taglio, allora anche il taglio deve variare (ha un salto, punto 2 dell’elenco precedente). Ecco ancora perché se non c’è carico distribuito (p(x) = 0), risulta M funzione lineare e T costante: seT’(x)=p(x)=0, T(x) ha la derivata nulla, e quindi è costante.
E’ molto importante apprendere bene le regole qui richiamate. Esse possono essere usate per un verso per controllare i diagrammi una volta che siano stati tracciati, per un altro verso possono aiutare a tracciare i diagrammi stessi, fornendo l’identikit del diagramma da tracciare.
Consideriamo il classico esempio seguente:
I diagrammi e le reazioni vincolari sono i seguenti:
Se dividiamo l’asta in un generico punto a distanza x dal primo estremo, e scriviamo l’equilibrio alla traslazione orizzontale, verticale ed alla rotazione intorno al punto di separazione dei due monconi, chiamando al solito V la reazione verticale di sinistra, H quella orizzontale di sinistra (nulla), otteniamo:
N+H=0
V-px - T= = 0
Vx-0.5px2-M=0
Risolto il sistema (che vale lungo tutta l’asta) si ottiene (V è nota e vale 0.5pL, H=0):
N(x)=0
T(x)=0.5pL-px
M(x)=0.5pLx-0.5px2
La rappresentazione grafica di queste curve è costituita dai diagrammi rappresentati nella figura precedente. Si noti che infatti ad esempio, M(L/2) = (1/8)pL2=0.125pL2.
Osserviamo che le regole enunciate sono soddisfatte: il momento varia parabolicamente, il taglio linearmente. Inoltre facendo la derivata di M(x) si ottiene:
M’(x)= 0.5pL-2(0.5px)= 0.5pL-px = T(x)
Come promesso dalla (1). E ancora come detto dalla (2)
p(x) = T’(x) = -p
Infine si osservi che la concavità del diagramma di momento è diretta verso l’alto, in verso opposto al segno del carico distribuito, diretto verso il basso (come previsto dalla (3)).
Sebbene l’uso del sistema di rompere l’asta evidenziando le azioni interne, per poi scrivere le equazioni di equilibrio in funzione di “x” e dei carichi attivi e reattivi applicati, sebbene questo metodo sia corretto, questo è un metodo abbastanza lungo, e pochi lo seguono nella pratica. Un corretto apprendimento delle regole enunciate ed un po’ di senso fisico (quando un’asta è tesa?) bastano spesso a risolvere il problema.
Vediamo la seguente sedia, e proviamo a calcolarne i diagrammi con questo altro metodo (ogni tratto è lungo L). Si richiede uno sforzo di concentrazione.
Muoviamoci a partire dall’alto e scendiamo lungo lo schienale. Se rompiamo idealmente in un punto qualsiasi di questo tratto e consideriamo la situazione del troncone superiore, vi è la sola forza orizzontale –2pL e le azioni interne a fare equilibrio. Poiché la forza è orizzontale ed il tratto considerato verticale, l’azione assiale in questo tratto è nulla. Il taglio deve essere costante (manca il carico distribuito) e, per equilibrio, non può che valere 2pL. Il segno è negativo. Il momento è dato da 2pL per la distanza x dall’estremo superiore, e quindi cresce linearmente a partire da 0, quando ci si trova proprio all’estremo (braccio nullo), fino ad arrivare a 2pL(L), quando ci si trova in basso, all’estremo del tratto considerato.
Ora percorriamo la seduta, da sinistra verso destra, chiamando x la distanza del punto generico in cui rompiamo dall’estremo di sinistra. Questa volta il tratto è orizzontale e si vede che la forza 2pL tende ad allungare la seduta, quindi provoca una trazione: N=+2pL. La forza 2pL non provoca alcun taglio sulla seduta perché è orizzontale. Invece, il carico distribuito provoca un taglio lineare che parte da 0 nell’estremo di sinistra, eppoi nel punto di rottura vale px (p per x). Il valore massimo sarà all’estremo di destra, quando varrà pL. Il segno è negativo. Consideriamo ora il momento. La forza 2pL ha un braccio L in tutti i punti della seduta e tende le fibre di sopra della stessa (tutto lo schienale ed il moncone di seduta ad esso attaccato tendono a ruotare in modo antiorario). Il carico distribuito, che nel punto considerato ha risultante px, ha un braccio pari a 0.5x (perché il suo risultante è applicato nel punto di mezzo del tratto caricato considerato: dall’estremo al punto in cui abbiamo rotto idealmente). Anch’esso fa ruotare il moncone in senso antiorario (povera sedia) quindi i due contributi si sommano M=2pL2+0.5px2, e tende le fibre di sopra. All’estremo di destra varrà 2.5pL2.
Da ultimo consideriamo il tratto verticale in basso. Qui avremo N=-pL, perche il tratto è schiacciato dal carico distribuito che ha risultante pL, mentre l’azione 2pL non entra in gioco perché orizzontale. Il taglio varrà invece proprio 2pL, perché è il carico distribuito, questa volta, a non entrare in gioco. Il momento va a tendere le fibre di destra ed è dato da due contributi (deve essere lineare perché non c’è più il carico distribuito): il contributo di 2pL che vale 2pL(L+x), avendo chiamato x la distanza del punto generico dall’estremo superiore del tratto considerato. Il contributo del carico distribuito, sempre eguale da punto a punto, che vale pL(L/2), con lo stesso segno dell’altro. Pertanto M=(5/2) pL2 + 2pLx. Il valore massimo si ha al piede ed è pari a (9/2)pL2= 4.5pL2.
A conferma di quanto detto, nella figura seguente sono dati i diagrammi che abbiamo calcolato: tutto torna.
E’ da notare che le azioni interne del punto al piede coincidono con le reazioni vincolari (se fossimo partiti dal basso anziché dall’alto avremmo proprio constatato questo fatto).
Immaginando di realizzare questa sedia con un tubo, i diagrammi ci dicono dove è il massimo momento flettente: al piede; la massima azione assiale: sulla seduta; il massimo taglio: sullo schienale e sulla gamba. Potremo così fare le nostre verifiche.